Economists like to emphasize how people and businesses will adapt to climate change. On a geological scale the world is warming very fast. But on a human scale it is warming slowly, so we can easily adjust infrastructure and management decisions to the gradually changing climate. For example, in agriculture farmers can gradually adjust planting times, cultivars, and locations where we grow crops, and so on.
So how much does adaptation really buy us? As it turns out, probably very little, at least in most contexts.
Since it is economists who often emphasize this point, sometimes even intimating that otherwise negative impacts could turn positive with adaptation, perhaps we should pause for a moment to consider what basic microeconomic theory says about it. And we have a ready-made tool for the job, called the envelope theorem (or here), that provides essential insight.
I'll try to make this intuitive, but it helps to be a little formal. Suppose agricultural yield is:
$ y = f(x, r) $
where $r$ indicates climate and $x$ represents farmers' decisions. I'm just using notation from a generic case in the second link above.
Farmers' decisions are not random. With time and experience, we should expect farmers to optimize decisions for their climate. Call these optimal decisions $x^*(r)$. So, the outcomes we observe in practice are
$ y^* = f(x^*(r), r) $
Now, to obtain a first-order approximation of the effect of climate change on yield, we need to find $\frac{dy^*}{dr}$, which is just a fancy way of saying the marginal change in observed yield for a small change in climate. Multiply this marginal change by the total change in climate (the change in $r$), and we get a first-order approximation to the total impact.
If you've taken basic calculus, you learned the chain rule, which says that:
$\frac{dy^*}{dr} = \frac{df}{dx} \frac{dx}{dr} + \frac{df}{dr}$
If the farmer is optimizing, however, $ \frac{df}{dx} = 0 $. The farmer cannot improve yield outcomes by changing decisions, because s/he's already optimizing. So
$ \frac{dy^*}{dr} = \frac{df}{dr} $
And this gives the heart of the envelope theorem: to a first approximation, we don't need to worry about changes in behavior ($\frac{dx}{dr}$, or adaptation) to evaluate the effect of a change in climate on output. The fact that behavior is already optimized means that behavioral adjustments will be second-order.
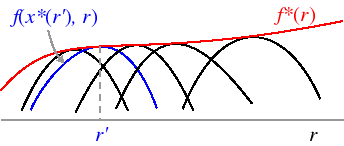
Here's an illustration of the math from lifted from the link above. The black and blue curves hold farmers's decisions fixed at different levels of $x$, optimized at each $r$ The $f^*(r)$ ( or $y^*$) we observe is the "upper envelope" of the all the blue and black curves with different, optimized levels of $x$.
Now, if $f^*(r)$ is highly nonlinear, and we are contemplating a very large change in climate, then adaptation will come into play. But even then it's probably not going to be a primary consideration.
I don't expect this basic insight, drilled into every economist during their first year of grad school (and even some undergraduates), will stop some economists from over-emphasizing adaptation. But our own basic theory nevertheless indicates it is a small deal. And it seems to me that the evidence so far bears this out just as clearly as the theory does.
I'll try to make this intuitive, but it helps to be a little formal. Suppose agricultural yield is:
$ y = f(x, r) $
where $r$ indicates climate and $x$ represents farmers' decisions. I'm just using notation from a generic case in the second link above.
Farmers' decisions are not random. With time and experience, we should expect farmers to optimize decisions for their climate. Call these optimal decisions $x^*(r)$. So, the outcomes we observe in practice are
$ y^* = f(x^*(r), r) $
Now, to obtain a first-order approximation of the effect of climate change on yield, we need to find $\frac{dy^*}{dr}$, which is just a fancy way of saying the marginal change in observed yield for a small change in climate. Multiply this marginal change by the total change in climate (the change in $r$), and we get a first-order approximation to the total impact.
If you've taken basic calculus, you learned the chain rule, which says that:
$\frac{dy^*}{dr} = \frac{df}{dx} \frac{dx}{dr} + \frac{df}{dr}$
If the farmer is optimizing, however, $ \frac{df}{dx} = 0 $. The farmer cannot improve yield outcomes by changing decisions, because s/he's already optimizing. So
$ \frac{dy^*}{dr} = \frac{df}{dr} $
And this gives the heart of the envelope theorem: to a first approximation, we don't need to worry about changes in behavior ($\frac{dx}{dr}$, or adaptation) to evaluate the effect of a change in climate on output. The fact that behavior is already optimized means that behavioral adjustments will be second-order.
Here's an illustration of the math from lifted from the link above. The black and blue curves hold farmers's decisions fixed at different levels of $x$, optimized at each $r$ The $f^*(r)$ ( or $y^*$) we observe is the "upper envelope" of the all the blue and black curves with different, optimized levels of $x$.
Now, if $f^*(r)$ is highly nonlinear, and we are contemplating a very large change in climate, then adaptation will come into play. But even then it's probably not going to be a primary consideration.
I don't expect this basic insight, drilled into every economist during their first year of grad school (and even some undergraduates), will stop some economists from over-emphasizing adaptation. But our own basic theory nevertheless indicates it is a small deal. And it seems to me that the evidence so far bears this out just as clearly as the theory does.