Economists like to emphasize how people and businesses will adapt to climate change. On a geological scale the world is warming very fast. But on a human scale it is warming slowly, so we can easily adjust infrastructure and management decisions to the gradually changing climate. For example, in agriculture farmers can gradually adjust planting times, cultivars, and locations where we grow crops, and so on.
So how much does adaptation really buy us? As it turns out, probably very little, at least in most contexts.
Since it is economists who often emphasize this point, sometimes even intimating that otherwise negative impacts could turn positive with adaptation, perhaps we should pause for a moment to consider what basic microeconomic theory says about it. And we have a ready-made tool for the job, called the envelope theorem (or here), that provides essential insight.
I'll try to make this intuitive, but it helps to be a little formal. Suppose agricultural yield is:
$ y = f(x, r) $
where $r$ indicates climate and $x$ represents farmers' decisions. I'm just using notation from a generic case in the second link above.
Farmers' decisions are not random. With time and experience, we should expect farmers to optimize decisions for their climate. Call these optimal decisions $x^*(r)$. So, the outcomes we observe in practice are
$ y^* = f(x^*(r), r) $
Now, to obtain a first-order approximation of the effect of climate change on yield, we need to find $\frac{dy^*}{dr}$, which is just a fancy way of saying the marginal change in observed yield for a small change in climate. Multiply this marginal change by the total change in climate (the change in $r$), and we get a first-order approximation to the total impact.
If you've taken basic calculus, you learned the chain rule, which says that:
$\frac{dy^*}{dr} = \frac{df}{dx} \frac{dx}{dr} + \frac{df}{dr}$
If the farmer is optimizing, however, $ \frac{df}{dx} = 0 $. The farmer cannot improve yield outcomes by changing decisions, because s/he's already optimizing. So
$ \frac{dy^*}{dr} = \frac{df}{dr} $
And this gives the heart of the envelope theorem: to a first approximation, we don't need to worry about changes in behavior ($\frac{dx}{dr}$, or adaptation) to evaluate the effect of a change in climate on output. The fact that behavior is already optimized means that behavioral adjustments will be second-order.
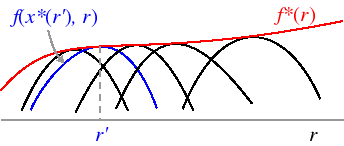
Here's an illustration of the math from lifted from the link above. The black and blue curves hold farmers's decisions fixed at different levels of $x$, optimized at each $r$ The $f^*(r)$ ( or $y^*$) we observe is the "upper envelope" of the all the blue and black curves with different, optimized levels of $x$.
Now, if $f^*(r)$ is highly nonlinear, and we are contemplating a very large change in climate, then adaptation will come into play. But even then it's probably not going to be a primary consideration.
I don't expect this basic insight, drilled into every economist during their first year of grad school (and even some undergraduates), will stop some economists from over-emphasizing adaptation. But our own basic theory nevertheless indicates it is a small deal. And it seems to me that the evidence so far bears this out just as clearly as the theory does.
I'll try to make this intuitive, but it helps to be a little formal. Suppose agricultural yield is:
$ y = f(x, r) $
where $r$ indicates climate and $x$ represents farmers' decisions. I'm just using notation from a generic case in the second link above.
Farmers' decisions are not random. With time and experience, we should expect farmers to optimize decisions for their climate. Call these optimal decisions $x^*(r)$. So, the outcomes we observe in practice are
$ y^* = f(x^*(r), r) $
Now, to obtain a first-order approximation of the effect of climate change on yield, we need to find $\frac{dy^*}{dr}$, which is just a fancy way of saying the marginal change in observed yield for a small change in climate. Multiply this marginal change by the total change in climate (the change in $r$), and we get a first-order approximation to the total impact.
If you've taken basic calculus, you learned the chain rule, which says that:
$\frac{dy^*}{dr} = \frac{df}{dx} \frac{dx}{dr} + \frac{df}{dr}$
If the farmer is optimizing, however, $ \frac{df}{dx} = 0 $. The farmer cannot improve yield outcomes by changing decisions, because s/he's already optimizing. So
$ \frac{dy^*}{dr} = \frac{df}{dr} $
And this gives the heart of the envelope theorem: to a first approximation, we don't need to worry about changes in behavior ($\frac{dx}{dr}$, or adaptation) to evaluate the effect of a change in climate on output. The fact that behavior is already optimized means that behavioral adjustments will be second-order.
Here's an illustration of the math from lifted from the link above. The black and blue curves hold farmers's decisions fixed at different levels of $x$, optimized at each $r$ The $f^*(r)$ ( or $y^*$) we observe is the "upper envelope" of the all the blue and black curves with different, optimized levels of $x$.
Now, if $f^*(r)$ is highly nonlinear, and we are contemplating a very large change in climate, then adaptation will come into play. But even then it's probably not going to be a primary consideration.
I don't expect this basic insight, drilled into every economist during their first year of grad school (and even some undergraduates), will stop some economists from over-emphasizing adaptation. But our own basic theory nevertheless indicates it is a small deal. And it seems to me that the evidence so far bears this out just as clearly as the theory does.



Mike,
ReplyDeleteThanks for posting this very interesting and clever piece! However, I'm not convinced that basic theory tells us that climate change adaptation won't be a big deal. In short, it seems like you've set up the problem such that farmers choose x to maximize output (y). But don't farmers maximize profits instead of output? If so, I'm worried that assuming otherwise leads us to ignore how price signals will induce farmers, consumers, and entrepreneurs to respond in ways that could mitigate the output and welfare consequences of climate change.
Here's a more lengthy discussion of the 3 questions I have about your post:
#1. Don't Farmers Maximize Profits Instead of Output?
You have set up the problem such that farmers employ x in order to maximize output (y). If this assumption is true, then there is an intuitive appeal to your result that adaptation to climate change won't matter much because farmers are already doing everything they can to make yields as big as possible. But is there any evidence to support this assumption? An alternative assumption would be that farmers seek to maximize profits instead. In that case, farmers could likely physically do more to increase yields (apply more fertilizer, pesticide, etc), but choose not to because the marginal benefits don't exceed the marginal costs at prevailing prices. However, this would change as the price of the farmer's output rises.
#2. Aren't Profit-Maximizing Farmers Sensitive to Higher Prices For Their Output?
Wouldn't we expect a climate-based supply shock to increase the prices of agricultural prices? If so, wouldn't farmers respond to higher prices by producing more output? If that is the case, this static supply-response alone could mitigate the impact of a climate-based supply shock on output and welfare more generally. However, sustained higher prices could induce responses from consumers and entrepreneurs that would further mitigate the consequences of climate change for human welfare.
#3. Won't Higher Prices Encourage Consumers to Find Substitutes and Entrepreneurs to Develop New Technologies?
If the price of some agricultural goods remains high for a long-period of time, we would expect that consumers will eventually substitute toward cheaper food stuffs. Similarly, the higher price of these crops will encourage entrepreneurs to either develop new and cheaper substitutes (hopefully there are better ideas out there than Soylent: http://en.wikipedia.org/wiki/Soylent_(food_substitute)) or new and cheaper ways to grow foods in different climates (i.e. genetically modifying crops to be less sensitive to drought).
Mike,
DeleteSince you were good enough to summarize your ideas in a formal model, I thought I would do the same. Specifically, I start from the assumption that farmers maximize profits instead of yields. In this case, a farmer's objective function would be:
maximize π = p*f(x, r) - wx
where p is the price of the output and w would be the price of generic input x.
Now, we could still use the envelope theorem. Specifically, if we take the derivative of the objective function with respect to price and evaluate it at its optimum we get output as a function of parameters: y* = f(p, r, w). This is just Hotelling's Lemma.
However, if we want to find dy/dr, we need need to (at least) specify a partial equilibrium model to take account of endogenous prices. I took a quick stab at doing that here:
Click Here
As you will see, under normal assumptions about supply and demand, we should only get your result that dy/dr = df/dr if farmers are totally unresponsive to price (a very strong assumption). Note that this does not take account for the more "dynamic" responses of consumers and entrepreneurs discussed above.
Dallas,
ReplyDeleteI see you point. But don't think adding prices changes the general conclusion very much.
I agree that price response is much more interesting and relevant than direct climate response. But if you look at the literature (say, starting from Mendelsohn, Nordhaus and Shaw, AER 1994), I think you'll find prices are mostly ignored (explicitly or implicitly held fixed) with the focus being mainly on direct adaptation to climate. Few are trying estimate price elasticities. Fewer emphasize price response as central. But I do, and I think you'll see that if you look at a few of my recent published and working papers.
Mike,
DeleteThanks for responding!
First, I agree with you it is possible that adding prices might not change the general conclusions very much as an empirical matter. For example, like I said earlier, if farmers are totally insensitive to price, they won't matter at all. Whether this is close to how the real world looks, you're obviously in a much better position to say. I will just note that the primary purpose of my comment was to note that we can't say this is the case based on theory alone.
Second, I actually had to read MNS (1994) in my environmental field course and while I didn't think about it then, I think you might be right that their approach might ignore the role of prices as discussed here. I'll have to re-read their paper and think about it a bit more.
Thanks for the exchange!
Dallas, Let me clarify: I don't think adding prices affects the general conclusion with respect to direct adaptation to climate (dy/dr). I fully agree with you that, in an equilibrium model, prices will change (dp/dr could be significant), and behavior to prices (dx/dp) will matter. But that's not the kind of adaptation many researchers and pundits are emphasizing.
DeleteJust read Mendelsohn et al.'s paper, and found it interesting. But can a cross-section regression analysis really answer the question about how people in the same place adapt to climate change over time? Another question: Following your post, if considering the broader economy (more than agriculture), can we say the climate damage is even smaller because people can better optimize their choices?
ReplyDeleteShameless self-promotion, but readers might be interested in a recent paper in Nature Climate Change that tries to estimate exactly this adaptation envelope for European agriculture using combinations of cross-sectional (for the outer envelope) and inter-temporal (inner envelope) variation: http://www.nature.com/nclimate/journal/v4/n7/full/nclimate2228.html
ReplyDeleteWe find this adaptation envelope seems to differ substantially between crops - small for wheat and barley but much larger for maize.
Thanks Fran. Shameless self promotion is fully acceptable here :-)
DeleteSorry I wasn't paying attention for awhile, and was late to moderate your comment. (I moderate comments more than 2 weeks old to help filter spam.)