Lunch break (for math/probability/statistics wonks):
So 11 of 12 jurors thought Blagojevich was guilty of selling a seat in the U.S. Senate. Assuming those jurors were a representative sample of the kind of jurors we might expect from a retrial, what are the odds he would be convicted if he were retried?
I see two ways of answering this question, one is pretty easy and the other, which has a Bayesian flair to it, is more difficult. The two answers are probably pretty similar, but I haven't done the harder and probably more appropriate one yet.
I'll post my answers later in the day. In the meantime, if you're up for a fun distraction you can tell me your answer in the comments.
Update: So the easy answer is obtained by assuming the probability of a "guilty" verdict juror is the frequentist estimate of 11/12, since in our sample of 12 jurors, one voted "not guilty." Then the probability of getting twelve "guilty" verdict jurors is (11/12)^12 = 0.352, or a 35.2% chance of conviction. Now that assumes a lot (I'll say more about assumptions at the end). But for now let's note that a frequentist would actually object to this answer because he/she would say that the true probability is unknowable, and thus would only say that the true probability of conviction on a retrial is between (9/12)^12 and (12/12)^12, or 3.2% and 100% with 95% confidence, which is not a very inspiring prediction.
So the only reasonable way to come with an actual probability of conviction on a retrial is to be a Bayesian. That means plugging in a "prior belief" for the odds of a randomly selected "guilty" voting juror before the first trial took place. Such a belief is subjective, which is philosophically problematic. But can't we come up with a reasonable, albeit subjective, prior? Or consider a range?
First, let's put down the key equation, which can be derived by combining the probability distribution of the binomial with Bayes rule, and is also given here on Wikipedia.
The notation here: p(a | m, n) is the distribution of the probability an individual juror will vote "guilty" given we have observed m of n jurors vote "guilty" in the first trial. So, m=11 and n=12. If we know p(a | 11, 12), we can calculate the probability of a guilty verdict on retrial as:
All we need now is p(a), the prior belief of a "guilty" voting juror, plug it into the Bayes relationship to find p(a|11,12), then solve the integral.
One commonly used prior is to assume a uniform distribution between 0 and 1. If you're not used to Bayesian analysis, this may seem strange, as we're assigning a probability distribution to a probability. That prior seems like a bad one here, because the prosecutors wouldn't have wasted their time on the initial trial if they weren't at least reasonably confident of a conviction. And if the prior belief of a guilty juror were uniform on (0,1), then the odds of conviction on the first trial would have been:
Which seems too small. So, how about we assume a prior distribution p(a) that would put the prior probability of conviction at 0.5. Yes, this is a wild assumption, but seems like a good starting point. Now with this one restriction we'll need a simple distribution with one parameter. A simple one is a polynomial distribution of the form p(a) = (z+1)a^z. If we select z such that
then it must be that z=11. So, plug all this in and it gives us a posterior probability of conviction equal to:
Or 43.8% chance of conviction on a retrial.
Now, if there weren't enough assumptions already, here are a few more. All of this assumes the retrial will be more or less like the initial trial, with a similar draw of jurors and the same presentation of evidence and defense.
But absent all of that, this geekish doodling suggests odds of conviction on the retrial look pretty similar, and perhaps slightly less, than they were perceived to be initially, at least if the initial belief of conviction was greater than 35% or so.
Wasn't that fun?
Subscribe to:
Post Comments (Atom)
Renewable energy not as costly as some think
The other day Marshall and Sol took on Bjorn Lomborg for ignoring the benefits of curbing greenhouse gas emissions. Indeed. But Bjorn, am...

-
The other day Marshall and Sol took on Bjorn Lomborg for ignoring the benefits of curbing greenhouse gas emissions. Indeed. But Bjorn, am...
-
The tragic earthquake in Haiti has had me wondering about U.S. Sugar policy. I should warn readers in advance that both Haiti and sugar pol...
-
A couple months ago the New York Times convened a conference " Food for Tomorrow: Farm Better. Eat Better. Feed the World ." ...
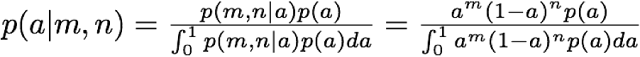




All I can say is the Obama administration could use a geek like you - if not the federal court system - looks like you could save us a few bucks....
ReplyDelete